Introduction: The Terahertz regime
The far-infrared (FIR) and mid-infrared (MIR) regions of the electromagnetic spectrum cover the frequency interval between approximately 0.1 THz and 100 THz (1 THz = 1012 Hz, corresponding to a photon energy of 4.1 meV). This regime is of critical importance for the fundamental understanding of various processes in condensed-matter systems. Eigenfrequencies of many elementary excitations are located within the THz band. Examples are collective oscillations of atoms in molecules and solids, plasmonic oscillations of free charge carriers in semiconductors [1], superconducting energy gaps [2], internal transitions of excitons in semiconductors and spin waves [3]. Ultrabroadband THz technology [4] provides the most direct method to investigate this regime. It gives access to the amplitude as well as the phase of the field transient on a timescale shorter than the duration of a single oscillation of light.

The Konstanz high-field THz source
An ideal THz emitter allows for the generation of relatively narrowband but tunable pulses consisting of only a few cycles of light, as well as the generation of extremely broadband pulses whose light field exhibits only a single oscillation of the electric field (single-cycle). One way to achieve this goal is the phase-matched optical rectification [5] of near-infrared femtosecond pulses (1 fs = 10-15 s) in the layered semiconductor GaSe. Crystals with a thickness in the order of 100 µm and less enable the generation of phase-stable mid-infrared pulses with a center frequency tunable between 10 THz and 40 THz by proper orientation of the birefringent GaSe crystal which fulfils the phase-matching conditions for a desired THz frequency.

A novel approach of a high-field THz source realized at the University of Konstanz allows us to enhance the quantum efficiency of the generation process by orders of magnitude. The hybrid concept combining an Er:fiber laser with a high-power Ti:sapphire amplifier enables phase-stable difference-frequency mixing of two near-infrared pulses. The mode-locked Er:fiber oscillator warrants a high stability of the hybrid system and seeds four parallel Er:fiber amplifiers. The radiation from one branch is frequency doubled and serves as a stable seed for the high-power Ti:sapphire amplifier with an output of 5 mJ at a repetition rate of 1 kHz. The laser output is split to pump two identical optical parametric amplifier (OPA) units with individually tunable signal wavelengths. The components of both amplifiers are superimposed for difference-frequency generation (DFG) in the nonlinear GaSe crystal. The clear advantage of this approach compared to the optical rectification can be seen at a first glance: The maximal THz frequency is not dependent on the bandwidth of the pump spectrum but can be flexibly adjusted via the relative frequency detuning of the two OPA units. It is only limited by phase-matching constraints in the emitter crystals. This scheme allows for the generation of transients with central frequencies tunable between 10 THz and 72 THz. The maximum peak electric field of these transients exceeds 100 MV/cm setting up the record for the most intense THz pulses detected electro-optically up to date [6, 7]. The peak THz power outnumbers large-scale facilities such as synchrotrons and free-electron lasers by more than four orders of magnitude. Furthermore, utilizing this setup we are capable to generate transients consisting of just a single oscillation of light [8]. Such intense ultrabroadband pulses form a perfect basis for nonlinear THz spectroscopy.
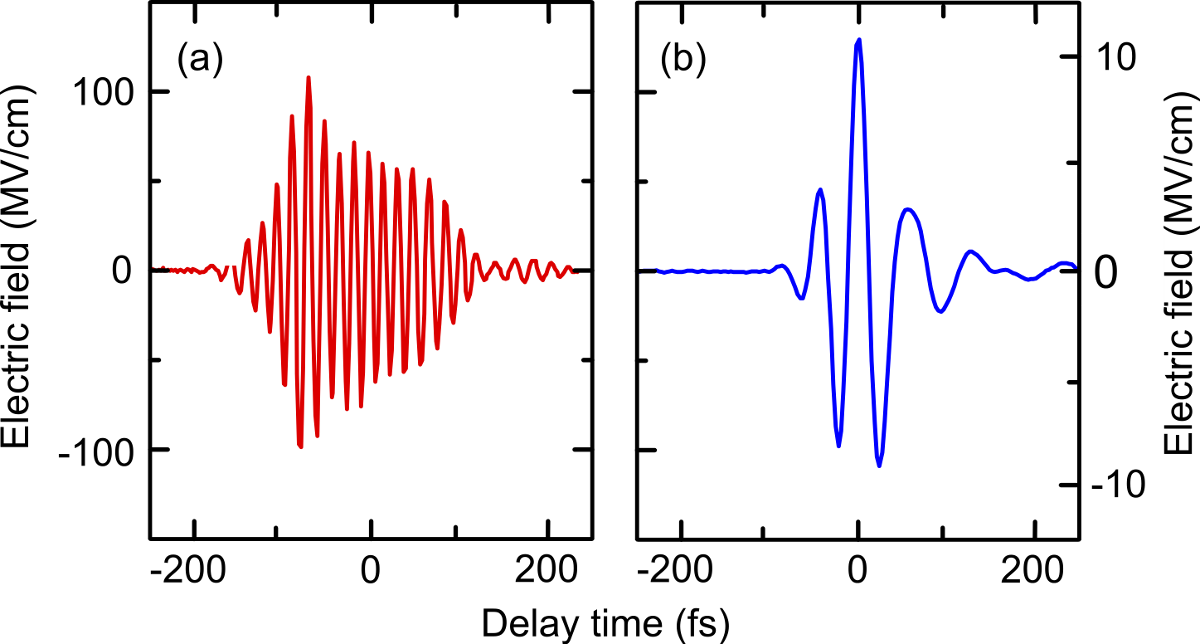
Applications: Nonlinear THz spectroscopy
The availability of intensive phase-stable multi-THz transients and ultrashort optical probe pulses enabling resolutions on a sub-cycle timescale open up opportunities for an entirely new class of ultrafast experiments. At the moment several projects are under way, for example:
(i) Coherent control of spin waves
Most nonlinear spectroscopy experiments rely on the interaction between the electric field of a THz pulse with electric dipoles of a system under study. However, the magnetic field of THz pulses can be also utilized in order to probe or control magnetic moments in a solid. In our recent work we have exploited the magnetic field of intense THz transients from our high-field source to coherently switch on and off a collective spin wave in an antiferromagnetic nickel oxide sample [3]. Using the magneto-optic Faraday effect we observe THz-driven spin precession in real time. In contrast to visible or near-infrared light, THz radiation can selectively couple to the magnetic degree of freedom with unprecedented speed, while leaving the other degrees of freedom unperturbed. Thus, the ultrafast and efficient control of the spin subsystem can be achieved without e.g. additional heating of the sample. Our findings are expected to enable new possibilities in ultrafast physics with modern materials such as high-temperature superconductors [9] and may inspire novel ideas for future information processing.
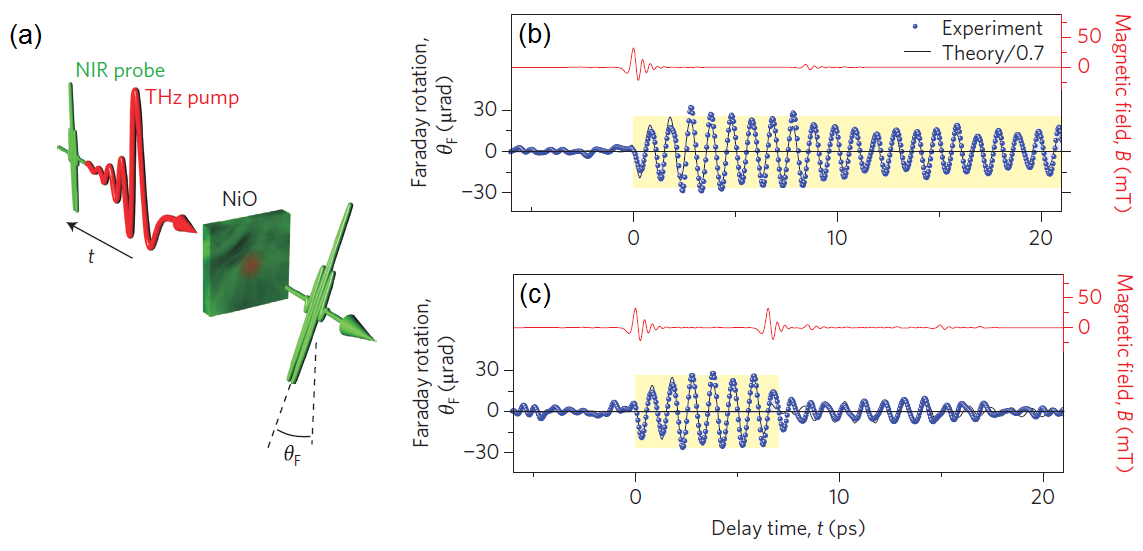
(ii) Two-dimensional THz spectroscopy:
Two-dimensional spectroscopy has been a powerful tool to examine coherent dynamics and coupling between different degrees of freedom in condensed matter systems. For example, studies in the near- (NIR) and mid-infrared (MIR) spectral region could provide insight into vibrational coupling and molecular structures of proteins as well as their dynamics. The expansion of the two-dimensional spectroscopy scheme to the THz spectral region is anticipated to provide access to coherent dynamics of fundamental low-energy excitations such as the inter-molecular motion in water or gap dynamics in superconductors.
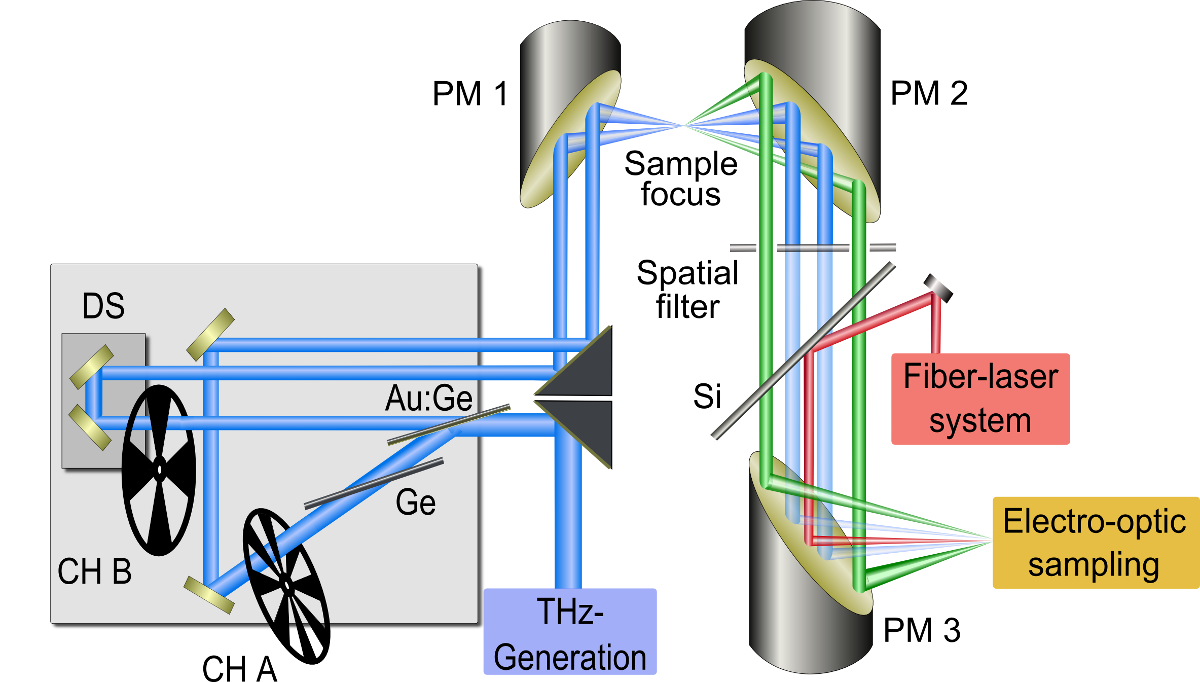
In the Konstanz high-field laboratory a broadband Mach-Zehnder interferometer in the THz spectral region was set up. By means of this interferometer the THz beam is split into two almost equally intense parts. One of those pulses can be delayed in respect to the other one by a delay stage. With this double-pulse sequence it is possible to perform multi-wave mixing experiments, such as four-wave mixing (FWM) in a so far inaccessible spectral region.
A FWM experiment is based on the following basic idea: The first pulse A generates a macroscopic polarization in the sample under study, which decays with the dephasing time. A second, temporally delayed pulse B incident on the sample still “sees” some contributions of the induced polarization of the first pulse, if the delay time τ between both transients is shorter than the dephasing time. In this case a nonlinear polarization grating is generated due to interference effects. The FWM signature consists of diffracted parts of pulse A or B from this grating.
A special case of a FWM experiment is the so called photon-echo experiment, which is the optically analogue to the spin-echo in nuclear magnetic resonance (NMR) spectroscopy. A simplified explanation of this class of experiments shall be given with the help of two-level systems, as we can describe the possible eigenstates by means of the so called Bloch sphere (Figure 6). Initially an ensemble of dipoles can be found in the ground state (time t0) and is excited by pulse A at time t1. If the sample under study is inhomogeneously broadened, the dipoles start to dephase (t1 < t < t2). At the time t2 another pulse B is incident on the sample and the dephased dipoles are rotated by the driving field, which simultaneously leads to a reversal of the precession. After the same delay time τ of the two pulses A and B all dipoles are in phase again and start to emit coherently which is known as a photon-echo. As the singular two-level systems have an intrinsic dephasing time, the intensity of the photon-echo signal decays for greater delay times τ. In contrast to the linear spectroscopy where inhomogeneous broadening is the dominating effect, one can observe the homogeneous broadening from the decay. This technique, thus, allows for the study of systems with a high disorder, such as fluids and molecular suspensions.
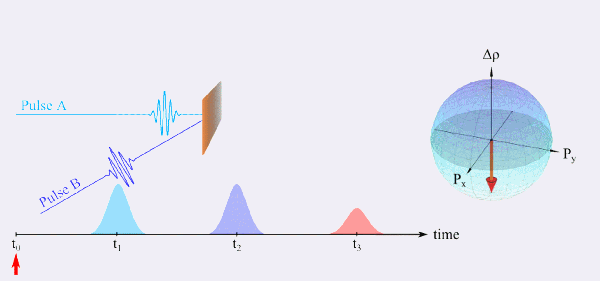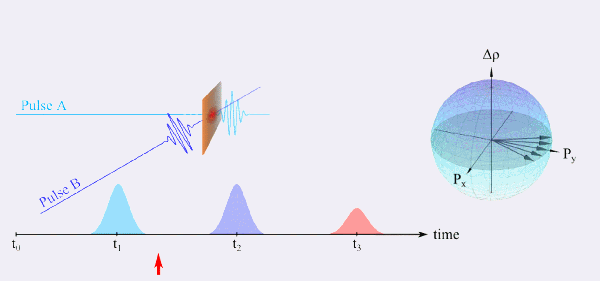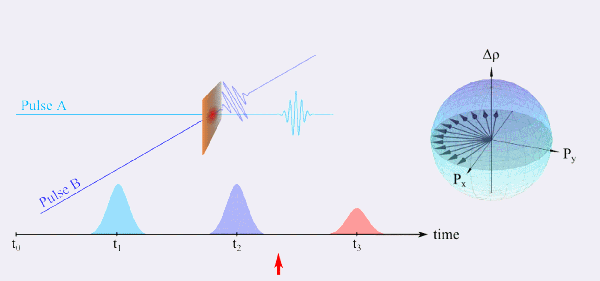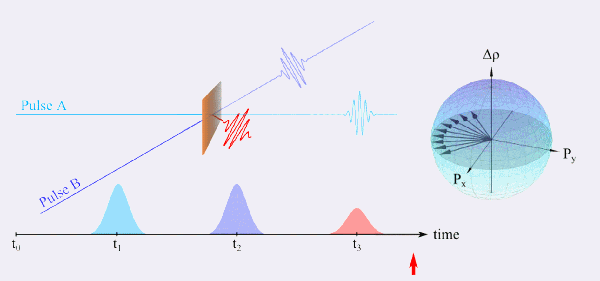
Only recently this setup was utilized to study coherent dynamics of the interband polarization of the bulk semiconductor indium antimonide (InSb). Even though the driving THz field possesses only half the frequency (and thus energy) of the band gap we were able to show that the system is driven into an extremely nonlinear regime where a perturbative description of the excitation is not sufficient any more [10]. Ongoing research and exciting questions, which will be examined by means of the setup presented above are the study of ultrafast dynamics and dephasing times of carbon-based materials, high-temperature superconductors and thin water films.
(iii) High-field effects in semiconductors
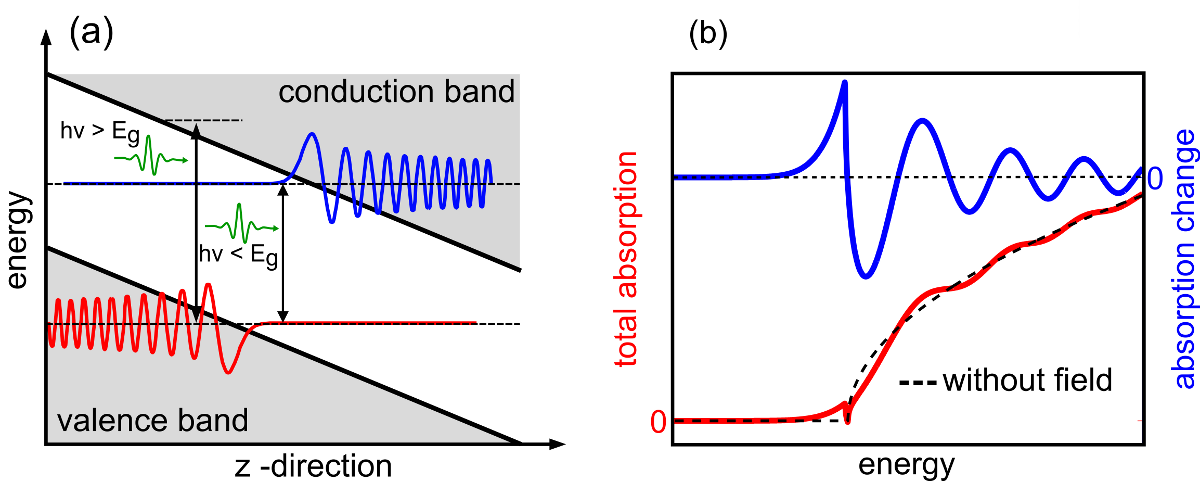
The continuous development of semiconductor-based electronics leads to an increasing miniaturization of the active device structures. The design of modern processor cores is based on micro-transistors with a gate length of only 22 nm. If a further doubling of the active elements per unit area according to Moor’s law is possible or limited by fundamental principles is subject of current research. However, it is a fact that the electric charges, namely electrons and holes, experience higher potential drops in smaller semiconductor structures. As a result, the related electric fields are of comparable magnitude to the inner-atomic binding energy (characteristic energy in semiconductors is 1 eV). Those strong electric fields lead to new physical phenomena and in consequence to a deviation of linear switching characteristics of the semiconductor devices. Examples are Zener tunneling, which is the crossing of an electron through a potential barrier by the quantum mechanical tunneling process, and impact ionization, where an electron can gain enough kinetic energy in an applied electric field to ionize a further electron by scattering processes. Those effects can lead to an avalanching increase of carriers and therefore to an extremely nonlinear response of semiconductor devices.

High-field effects in semiconductors treat transport properties of electronic carriers in extremely strong potential drops and the modification of the electronic wave function due to the applied electric field. Free electrons in the conduction band are accelerated ballistically and can reach high-energetic states in the band structure until scattering sets in (typically in the order of 10 fs to 1 ps) [11]. Related phenomena are inter-valley scattering and Bloch oscillations.
From the quantum mechanical view the additional potential term leads to a modification of Schrödinger’s equation [12]. The broken symmetry in direction of the electric field indicates that instead of Bloch waves Airy functions describe the probability amplitude of the electrons. In first order this influence can be regarded as a spatial tilting of the band structure. However, for increasing electric field this picture is not justified any more. Fields in the same order of magnitude as the inner atomic binding energy lead to a strong localization at the ion cores, which can be described by Wannier functions. The discreet character of the atoms becomes more and more dominant and may be observed as the so-called Wannier-Stark ladder in the absorption spectrum [13].
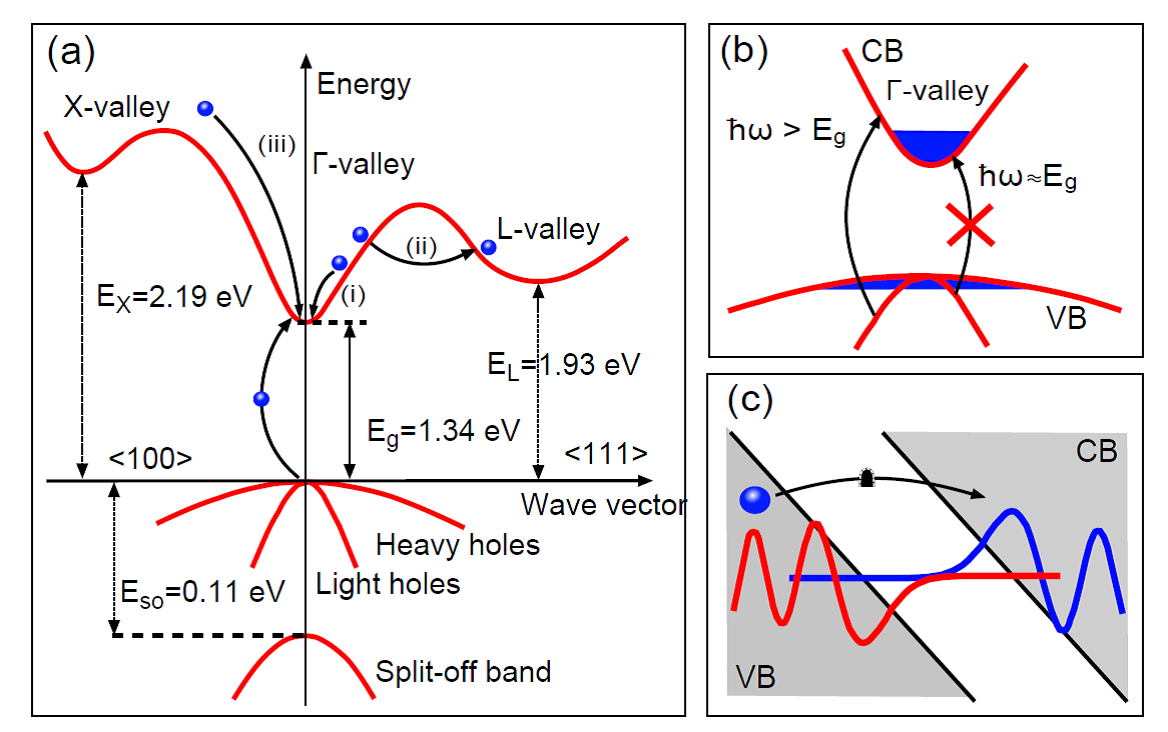
The observation of high-field phenomena in semiconductors with static electric fields is limited by the dielectric breakdown of the material, which is in general of the order of 100 kV/cm. An elegant method to reach higher internal field strength is to employ the electric field of ultrashort, intensive laser pulses [14]. The photon energy of these pulses has to be significantly below the electronic interband resonance to avoid absorption. In this situation far-off resonance the field influence can be described either as a classical electric field or as a multi-photon transition. A measure to decide which description is appropriate is given by the so called ponderomotive energy [15]. This energy describes the kinetic energy of a conduction band electron gained during one oscillation period. If the ponderomotive energy is higher than the photon energy non-perturbative high-field phenomena are predominant.
The high-field source at the University of Konstanz is capable of generating phase-locked, ultrashort multi-THz pulses, which are especially suitable to maximize the ponderomotive energy and therefore to observe high-field phenomena in semiconductors [7, 8]. The THz pulses are applied quasi-statically on the sample. They are temporally as well as spatially overlapped with an ultrashort and extremely broadband probe pulse. The relative transmission change of this probe pulse through the sample provides information about the THz induced modification of the dielectric properties of the material and, thus, about the superposition of electronic wave function and electromagnetic field. The delay between THz and probe pulse allows studying the temporal behavior, a monochromator to analyze the spectrally-resolved response. The broadband, ultrashort sub-10-fs probe pulse and the additional electro-optic detection enable highly resolved measurements of the transmission change in the order of a few femtoseconds.
In current experiments the technologically important high-speed semiconductors gallium arsenide (GaAs) and indium phosphide (InP) are under study. A variety of interesting phenomena is observed. The intense electric field leads to an instantaneous decrease of the transmission of photons with less energy and to an induced transmission of photons with higher energy than the band gap energy. These signatures are strong indications for an observation of the dynamically observed Franz-Keldysh effect [16]. Furthermore, the efficient generation of free carriers by tunneling and impact ionization is shown. The resulting high densities lead to signatures of electron dynamics on longer timescales, i.e. band gap renormalization and Pauli blockade.
References
[1] R. Huber, F. Tauser, A. Brodschelm, M. Bichler, G. Abstreiter und A. Leitenstorfer
"How many-particle interactions develop after ultrafast excitation of an electron–hole plasma"
Nature 414, 286 (2001)
[2] A. Pashkin, M. Porer, M. Beyer, K. W. Kim, A. Dubroka, C. Bernhard, X. Yao, Y. Dagan, R. Hackl, A. Erb, J. Demsar, R. Huber und A. Leitenstorfer
"Femtosecond Response of Quasiparticles and Phonons in Superconducting YBa2Cu3O7-δ Studied by Wideband Terahertz Spectroscopy"
Phys. Rev. Lett. 105, 067001 (2010)
[3] T. Kampfrath, A. Sell, G. Klatt, A. Pashkin, S. Mährlein, T. Dekorsy, M. Wolf, M. Fiebig, A. Leitenstorfer und R. Huber
"Coherent terahertz control of antiferromagnetic spin waves"
Nature Photon. 5, 31 (2010)
[4] C. Kübler, R. Huber und A. Leitenstorfer (eingeladener Artikel)
"Ultrabroadband terahertz pulses: generation and field-resolved detection"
Semicond. Sci. Technol. 20, 128 (2005)
[5] R. Huber, A. Brodschelm, F. Tauser und A. Leitenstorfer
"Generation and field-resolved detection of femtosecond electromagnetic pulses tunable up to 41 THz"
Appl. Phys. Lett. 76, 3191 (2000)
[6] A. Sell, A. Leitenstorfer und R. Huber
"Phase-locked generation and field-resolved detection of widely tunable terahertz pulses with amplitudes exceeding 100 MV/cm"
Opt. Lett. 33, 2767 (2008)
[7] A. Sell, R. Scheu, A. Leitenstorfer und R. Huber
"Field-resolved detection of phase-locked infrared transients from a compact Er:fiber system tunable between 55 and 107 THz"
Appl. Phys. Lett. 93, 251107 (2008)
[8] F. Junginger, A. Sell, O. Schubert, B. Mayer, D. Brida, M. Marangoni, G. Cerullo, A. Leitenstorfer und R. Huber
"Single-cycle multiterahertz transients with peak fields above 10 MV/cm"
Opt. Lett. 35, 2645 (2010)
[9] K. W. Kim, A. Pashkin, H. Schäfer, M. Beyer, M. Porer, T. Wolf, C. Bernhard, J. Demsar, R. Huber und A. Leitenstorfer
"Ultrafast transient generation of spin-density-wave order in the normal state of BaFe2As2 driven by coherent lattice vibrations"
Nature Materials 11, 497 (2012)
[10] F. Junginger, B. Mayer, C. Schmidt, O. Schubert, S. Mährlein, A. Pashkin, R. Huber und A. Leitenstorfer
wird publiziert
[11] A. Leitenstorfer, S. Hunsche, J. Shah, M. C. Nuss und W. H. Knox
"Femtosecond Charge Transport in Polar Semiconductors"
Phys. Rev. Lett. 82, 5140 (1999)
[12] Y. Yacoby
"High-Frequency Franz-Keldysh Effect"
Phys. Rev. 169, 610 (1968)
[13] G. H. Wannier
"Dynamics of Band Electrons in Electric and Magnetic Fields"
Rev. Mod. Phys. 34, 645 (1962)
[14] A. H. Chin, O. G. Calderon und J. Kono
"Extreme Midinfrared Nonlinear Optics in Semiconductors"
Phys. Rev. Lett. 86, 3292 (2001)
[15] K. Nordstrom et al.
"Excitonic Dynamical Franz-Keldysh Effect"
Phys. Rev. Lett. 81, 457 (1998)
[16] P. Y. Yu, und M. Cardona
"Fundamentals of Semiconductors"
Fourth Edition Springer, Berkely, CA and Stuttgart, Germany (March 2010)
