Einleitung: Das THz-Regime
Der ferninfrarote (FIR) und mittelinfrarote (MIR) Bereich des elektromagnetischen Spektrums umfasst das Frequenzintervall zwischen etwa 0,1 THz und 100 THz (1 THz = 1012 Hz, entspricht einer Photonenenergie von 4,1 meV). Dieses Regime ist für das Verständnis wichtiger Prozesse in der kondensierten Materie von zentraler Bedeutung: Viele Elementaranregungen weisen Eigenfrequenzen auf, welche im THz-Band liegen. Beispiele sind kollektive Schwingungen der Atome in Molekülen und Festkörpern, Dichteoszillationen von Ladungsträger-Plasmen in Halbleitern [1], supraleitende Bandlücken [2], interne Übergänge von Exzitonen in Halbleitern und Spinwellen [3]. Die direkteste Methode zur Untersuchung dieses Regimes bietet die ultrabreitbandige THz-Technologie [4], mit der Amplitude und Phase des elektrischen Feldes auf einer Zeitskala kürzer als die Dauer einer einzelnen Lichtschwingung zugänglich sind.

Die Hochfeld-Terahertz-Quelle
Ein idealer THz-Emitter ermöglicht sowohl die Erzeugung relativ schmalbandiger und abstimmbarer Impulse, die einige Lichtschwingungen enthalten, als auch die Erzeugung extrem breitbandiger Transienten, bei denen das Lichtfeld nur eine einzige Lichtschwingung (engl. single-cycle) ausführt. Eine Methode der Realisation ist die phasenangepasste optische Gleichrichtung [5] nahinfraroter fs-Impulse (1 fs = 10-15 s) im Schichthalbleiter GaSe. Kristalle einer Dicke in der Größenordnung von 100 µm und darunter ermöglichen die Erzeugung phasenstabiler mittelinfraroter Impulse mit Zentralfrequenzen zwischen 10 THz und 40 THz.

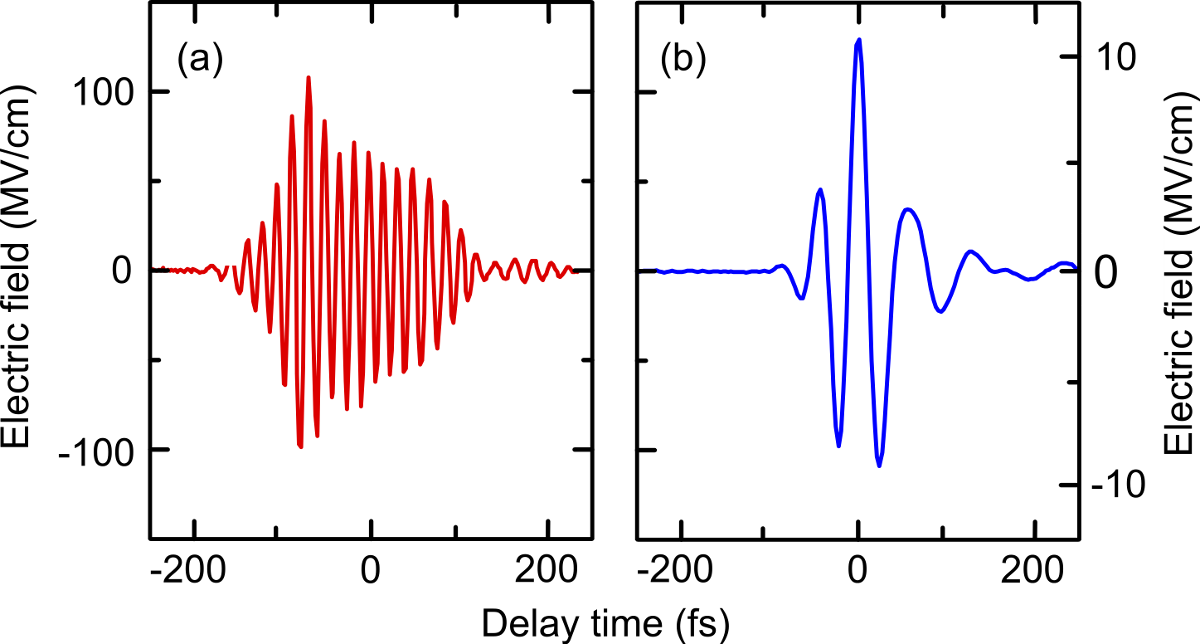
Mit der Hochfeld-Terahertz-Quelle der Universität Konstanz ist es möglich, diesen Bereich deutlich zu erweitern und gleichzeitig die Quanteneffizienz des Generationsprozesses um mehrere Größenordnungen zu erhöhen. Ein neuartiges Konzept, das einen Faserlaser mit einem leistungsfähigen Ti:Saphir-Verstärker verbindet, ermöglicht phasenstabile Differenzfrequenz-Mischung von zwei NIR-Impulsen. Der modengekoppelte Er:Faser-Oszillator sorgt für eine hohe Stabilität des Gesamtsystems und speist vier parallele Er:Faser-Verstärker. Einer dieser vier Zweige wird frequenzverdoppelt und in einem Ti:Saphir-Lasersystem auf eine Impulsenergie von 5 mJ bei einer Repetitionsrate von 1 kHz verstärkt. Dieser Impuls wird anschließend aufgespalten, um zwei identische optisch-parametrische Verstärker (engl. optical parametric amplifer; kurz: OPA) zu pumpen. Die Frequenzen der beiden Ausgangsimpulse lassen sich unabhängig voneinander einstellen. In einem nichtlinearen Kristall werden diese Impulse überlagert, so dass die Differenzfrequenz generiert wird. Der große Vorteil gegenüber der optischen Gleichrichtung ist sofort ersichtlich: Die maximale THz-Frequenz ist hier nicht mehr abhängig von der Bandbreite des Pumpspektrums, sondern kann flexibel über die relative Frequenzverstimmung der beiden OPAs eingestellt werden. Dies ermöglicht die Erzeugung von Impulsen mit Zentralfrequenzen zwischen 10 THz und 72 THz, sowie Spitzenfeldstärken von mehr als 100 MV/cm [6, 7]. Die zugehörigen Spitzenintensitäten übersteigen die bisherigen Rekordwerte von Großforschungseinrichtungen wie zum Beispiel Synchrotrons oder Freie-Elektronenlaser um bis zu vier Größenordnungen. Weiterhin können mit diesem System Transienten erzeugt werden, deren Lichtfeld aus einer einzelnen Licht-schwingung besteht [8]. Dies ist gerade im Hinblick auf die nichtlineare THz-Spektroskopie von großem Interesse.
Anwendungen: Nichtlineare THz-Spektroskopie
Die Verfügbarkeit phasenstabiler Impulse im Bereich von mehreren Terahertz mit höchsten Spitzenfeldstärken zusammen mit dem direkten Zugang zur Amplitude des Lichtfeldes erschließt eine völlig neue Klasse von Experimenten in der Ultrakurzzeit-Physik. Aktuell werden verschiedene Experimente durchgeführt, wie zum Beispiel:
(i) Kohärente Kontrolle von THz-Spinwellen
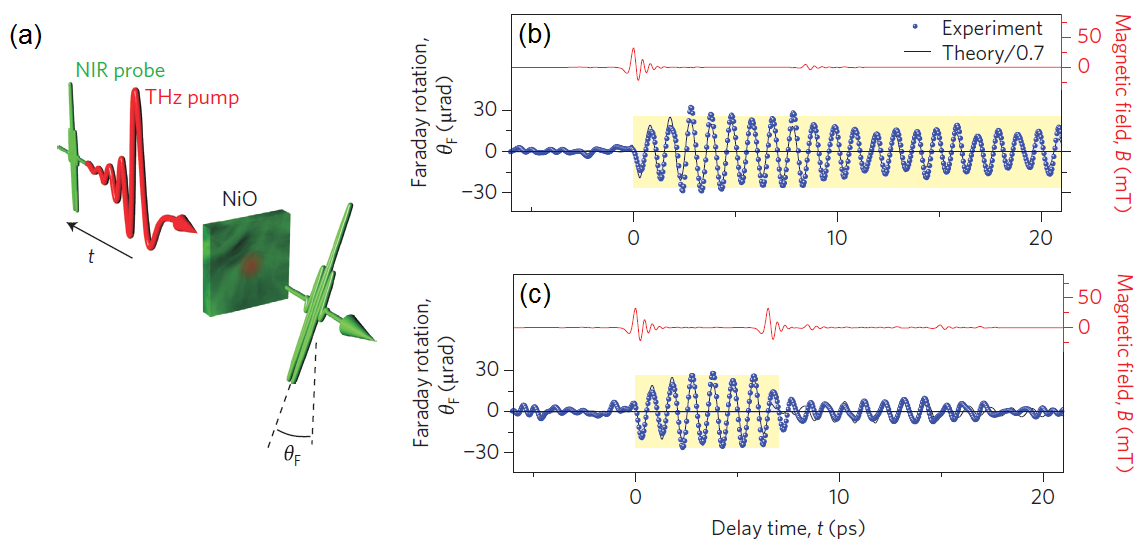
Die meisten Experimente der nichtlinearen Spektroskopie basieren auf der Wechselwirkung zwischen dem elektrischen Feld eines THz-Impulses und den elektrischen Dipolen des zu untersuchenden Systems. Allerdings lässt sich auch das Magnetfeld der THz-Impulse nutzen, um magnetische Momente in einem Festkörper anzuregen oder zu kontrollieren. Erst kürzlich konnten mit dem magnetischen Feld intensiver THz-Transienten unserer Hochfeld-Terahertz-Quelle kollektive Spinwellen in antiferromagnetischem Nickeloxid kohärent ein- und ausgeschaltet werden [3]. Im Gegensatz zu sichtbarem oder nahinfrarotem Licht kann die THz-Strahlung selektiv ausschließlich an den magnetischen Freiheitsgrad mit beispielloser Geschwindigkeit koppeln, während die anderen Anregungen nicht beeinflusst werden. So kann die ultraschnelle und effiziente Steuerung des Spin-Subsystems ohne Aufheizung der Probe erreicht werden. Diese Ergebnisse eröffnen neue Möglichkeiten für die Ultrakurzzeitphysik an modernen Materialien wie zum Beispiel Hochtemperatur-Supraleiter [9] und können weiterführende Ideen für die Informationsverarbeitung der Zukunft anregen.
(ii) Zweidimensionale THz-Spektroskopie:
Für die Untersuchung kohärenter Dynamiken und der Kopplung zwischen verschiedenen Freiheitsgraden in kondensierter Materie stellt die zweidimensionale Spektroskopie ein effizientes Verfahren dar. Beispielsweise konnten Experimente im nah- (NIR) und mittelinfraroten (MIR) Spektralbereich Einblick in eine Vielzahl von molekularen Vibrationsschwingungen und Strukturen von Proteinen sowie deren Dynamik geben. Mittels einer Erweiterung der zweidimensionalen Spektroskopie auf den THz-Spektralbereich erhofft wir uns einen direkten Zugang zu kohärenten Dynamiken von fundamentalen niederenergetischen Anregungen wie zum Beispiel den intermolekularen Schwingungen in Wasser oder dem Ordnungsparameter von Supraleitern.
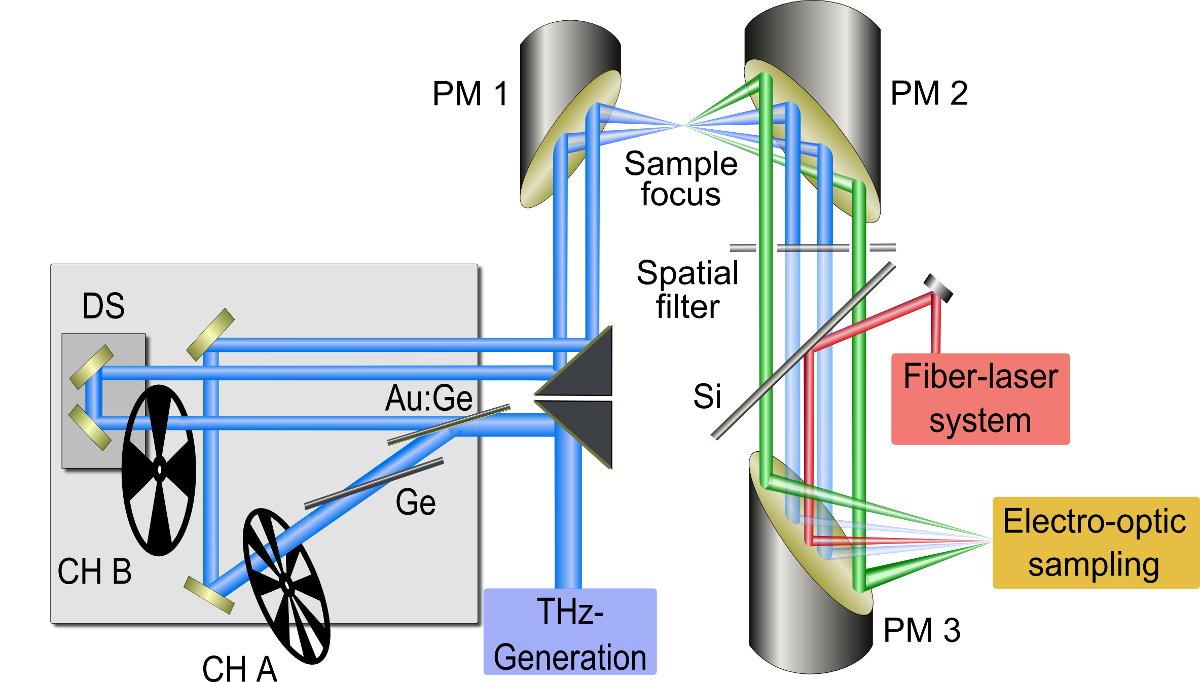
Im Hochfeldlabor der Universität Konstanz konnte ein breitbandiges Mach-Zehnder-Interferometer im THz-Spektralbereich aufgebaut werden. Mit diesem Interferometer wird der THz-Strahl in zwei annähernd gleich intensive Impulse aufgespalten. Ein Impuls lässt sich mittels eines Verschiebetisches zeitlich gegenüber dem anderen verzögern. Mit dieser Doppelimpulssequenz ist es möglich, Multi-Wellen-Misch-Experimente wie z.B. Vier-Wellen-Mischen (engl. four-wave mixing, kurz: FWM) in einem dafür bisher unzugänglichen Spektralbereich durchzuführen.
Ein FWM-Experiment basiert auf der folgenden grundsätzlichen Idee: Ein erster Impuls A erzeugt eine makroskopische Polarisation in der zu untersuchenden Probe, die mit der Dephasierungszeit abklingt. Ein zweiter Impuls B, der (zeitverzögert) auf die Probe trifft, „sieht“ noch einen Teil der vom ersten Impuls induzierten Polarisation, sofern die Verzögerungszeit τ der beiden Impulse kleiner als die Dephasierungszeit ist. In diesem Fall wird durch Interferenz ein nichtlineares Polarisationsgitter erzeugt. Das FWM Signal besteht aus an diesem Gitter gebeugten Anteilen von Impuls A oder B.
Ein Spezialfall eines FWM-Experiments ist das sogenannte Photon-Echo-Experiment, was das optische Analogon zum Spin-Echo der Kernspinresonanz-Spektroskopie (NMR) darstellt. Eine einfache Beschreibung dieses Experiments soll anhand von Zwei-Niveau-Systemen erfolgen, da sich so die möglichen Zustände mit Hilfe einer sogenannten Blochkugel darstellen lassen (Abbildung 6). Ein Ensemble von Dipolen befindet sich anfänglich im Grundzustand (Zeit t0) und wird zur Zeit t1 durch einen Impuls A angeregt. Ist die Probe inhomogen verbreitert, dephasieren die einzelnen Dipole (t1 < t < t2). Zur Zeit t2 treibt ein weiterer Impuls B die Probe und die dephasierten Dipole werden durch das angelegte Feld gedreht, was auch zu einer Umkehrung der Präzession führt. Nach der gleichen Verzögerungszeit τ der beiden Impulse A und B sind alle Dipole wieder in Phase und strahlen kohärent ab, was als Photon-Echo bezeichnet wird. Da die einzelnen Zwei-Niveau-Systeme eine intrinsische Dephasirungszeit haben, nimmt die Intensität vom Photon-Echo-Signal für größere Verzögerungszeiten τ ab. Im Gegensatz zur linearen Spektroskopie, wo die inhomogene Verbreiterung dominiert, ergibt sich aus dieser Abnahme die homogene Verbreiterung. Dieses Verfahren ermöglicht so die Untersuchung von Systemen mit hoher Unordnung, wie beispielsweise Flüssigkeiten und molekulare Strukturen.
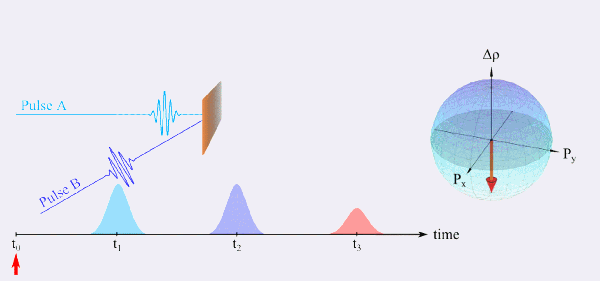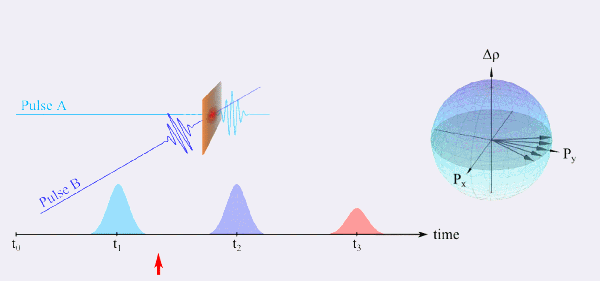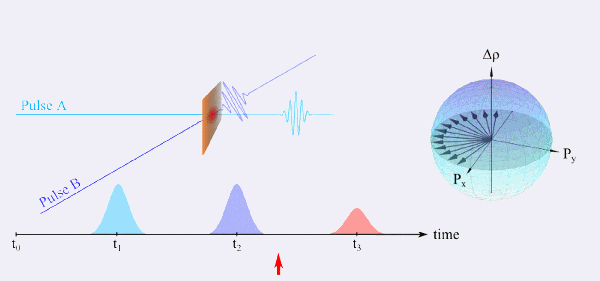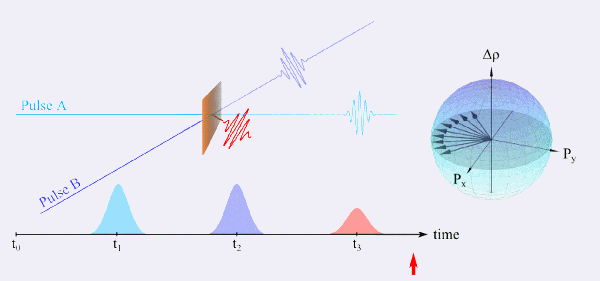
Dieser Aufbau konnte bereits zur Untersuchung der kohärenten Dynamik der Interband-Polarisation des Volumenhalbleiters Indiumantimonid (InSb) genutzt werden. Obwohl das treibende THz-Feld nur etwa die halbe Frequenz (und damit Energie) der Bandlücke besitzt, konnte gezeigt werden, dass das System in ein extrem nichtlineares Regime getrieben wird und eine perturbative (störungstheoretische) Beschreibung der Anregung nicht mehr ausreichend ist [10]. Weitere spannende und aktuelle Forschungsfragen, die mit diesem Aufbau untersucht werden können, sind ultraschnelle Dynamiken und Dephasierungen in kohlenstoffbasierten Materialien, Hochtemperatursupraleitern und dünnen Wasserfilmen.
(iii) Halbleitermaterialien unter dem Einfluss höchster elektrischer Felder
Die voranschreitende Entwicklung der halbleiterbasierten Mikroelektronik führt zu einer zunehmenden Miniaturisierung der Schaltelemente. Die Architektur moderner Prozessorkerne basiert auf Mikrotransistoren mit einer Gategröße von lediglich 22 nm. Ob eine weitere Verdopplung der aktiven Elemente pro Flächeneinheit entsprechend dem Mooreschen Gesetz möglich realisierbar ist oder an fundamentalen Naturgesetzen scheitert, ist Gegenstand aktueller Forschung. Fakt ist jedoch, dass Elektronen in kleineren Halbleiterstrukturen ein größeres Potentialgefälle überwinden müssen. Infolge dessen sind die damit verknüpften elektrischen Feldstärken im Vergleich zur inner-atomaren Bindung der Elektronen (Charakteristische Energie in Halbleitern ist 1 eV) nicht mehr vernachlässigbar klein. Felder solcher Stärke führen zu einer Reihe neuer, physikalisch interessanter Phänomene und daher zu Abweichungen der klassischen Schaltcharakteristik von Halbleiterbauelementen. Beispiele hierfür sind das Zener-Tunneln, bei dem ein Elektron eine Potentialbarriere durch den quantenmechanischen Tunnelprozess überwinden kann, und die Stoßionisation, bei der ein freies Elektron im Leitungsband genügend kinetische Energie im äußeren Feld aufnehmen kann, um ein weiteres Elektron durch einen Stoß zu ionisieren. Diese beiden Effekte können zu einer lawinenartigen Zunahme von Ladungsträgern und damit zu einem extrem nichtlinearen Verhalten von Halbleiterbauelementen führen.

Die Hochfeldphysik von Halbleitermaterialien beschäftigt sich mit den Transporteigenschaften von freien Ladungsträgern in extrem großen Potentialgefällen und der Modifikation der elektronischen Wellenfunktionen durch das äußere elektrische Feld. Da Streuprozesse zeitverzögert einsetzen (typischerweise im Bereich von > 100 fs – 1 ps) werden die Ladungsträger im elektrischen Feld ballistisch beschleunigt und können damit hochenergetische Zustände der Bandstruktur erreichen [11]. Hiermit verknüpfte Effekte sind Seitentaltransfer und Bloch-Oszillationen. Quantenmechanisch bedeutet ein zusätzlicher Potentialterm eine Modifikation der Schrödinger-Gleichung [12]. Der Symmetriebruch in Richtung des elektrischen Feldes führt dazu, dass nicht mehr Bloch-Wellen sondern Airy-Funktionen die Wahrscheinlichkeitsamplitude der Elektronen beschreiben. In erster Ordnung kann dieser Einfluss als Verkippung der Bandstruktur betrachtet werden. Für zunehmende elektrische Felder ist dieses Bild jedoch nicht mehr gerechtfertigt. Felder in der Größenordnung der inner-atomaren Bindungsstärke führen zu einer zunehmenden Lokalisierung der Elektronen, die dann durch Wannier-Funktionen beschrieben werden. Der diskrete Charakter der elektronischen Energiezustände tritt dann wieder hervor und sollte als sogenannte Wannier-Stark-Leiter im Absorptionsspektrum beobachtet werden können [13].
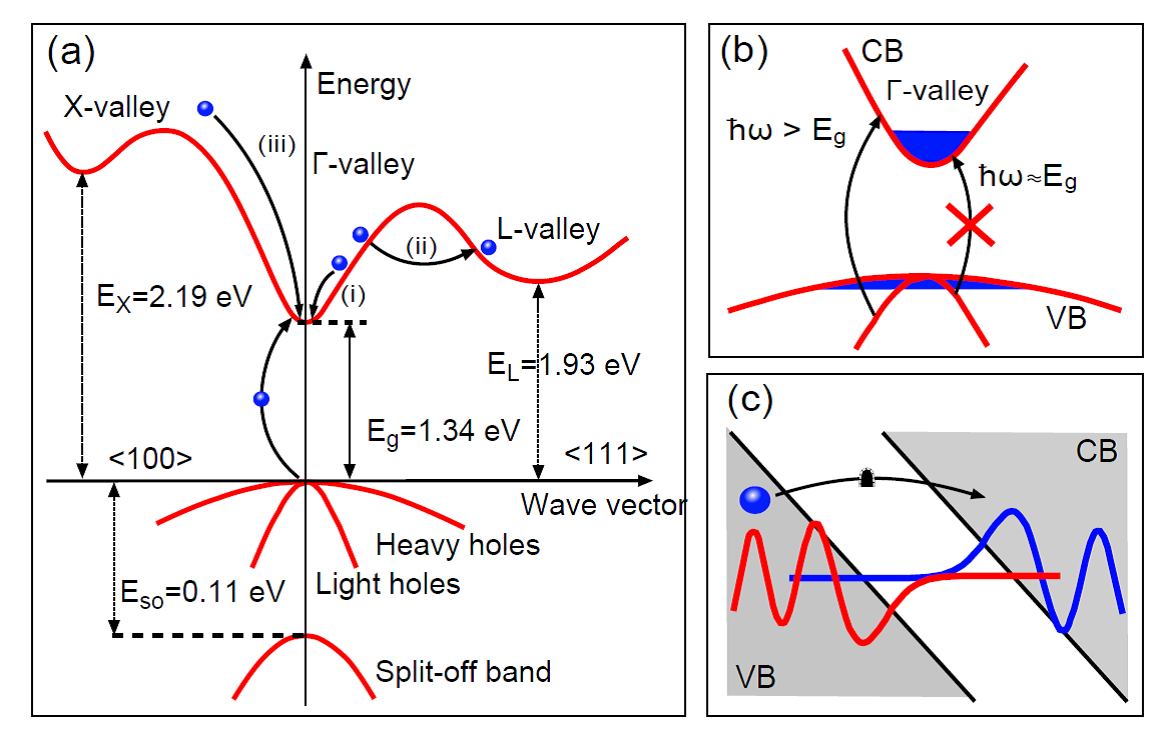
Die Untersuchung von Hochfeldeffekten in Halbleitern mit statischen elektrischen Feldern ist durch die Zerstörspannung des dielektrischen Durchbruchs beschränkt, die typischerweise im Bereich von 100 kV/cm liegt. Eine elegante Methode höhere Feldstärken zu erreichen ist die Verwendung des elektrischen Feldes von ultrakurzen, hoch intensiven Laserimpulsen [14]. Die Photonenenergie dieser Impulse muss dabei deutlich unterhalb der elektronischen Interband-Resonanz liegen, um eine Absorption zu vermeiden. Ein kritisches Maß für die Beurteilung, ob Ein- bzw. Multi-Photonen-Absorption oder der klassische Feldcharakter überwiegt, ist über die sogenannte „ponderomotive Energie“ gegeben [15]. Diese beschreibt die durchschnittliche kinetische Energie, die ein Leitungsbandelektron während einer Oszillationsperiode des elektrischen Feldes aufnehmen kann. Ist diese kinetische Energie größer als die Photonenenergie sind Hochfeldeffekte besonders dominant.
Die Hochfeldquelle in Konstanz generiert phasenstabile, ultrakurze Multi-THz-Impulse, die besonders geeignet sind um die ponderomotive Energie zu maximieren und somit Hochfeldeffekte in Halbleitern zu beobachten [7, 8]. Die THz-Impulse werden quasi-statisch an einer Halbleiterprobe angelegt und zeitlich sowie räumlich mit einem Abtastimpuls überlappt. Die Transmissionsänderung dieses Abtastimpulses durch die Probe gibt Auskunft über die Modifikation der dielektrischen Eigenschaften des Materials und damit über den Superpositionszustand aus elektronischem System und elektromagnetischem Feld. Über die Verzögerung zwischen Abtast- und THz-Impuls kann das zeitliche Verhalten, sowie mit Hilfe eines Monochromators die frequenzabhängige Antwort studiert werden. Der breitbandige, ultrakurze sub-10-fs-Abtastimpuls und die simultane elektro-optische Detektion über einen weiteren Impuls (Gateimpuls) ermöglicht eine zeitlich hochaufgelöste Messung der Transmissionsänderung im Bereich weniger Femtosekunden.
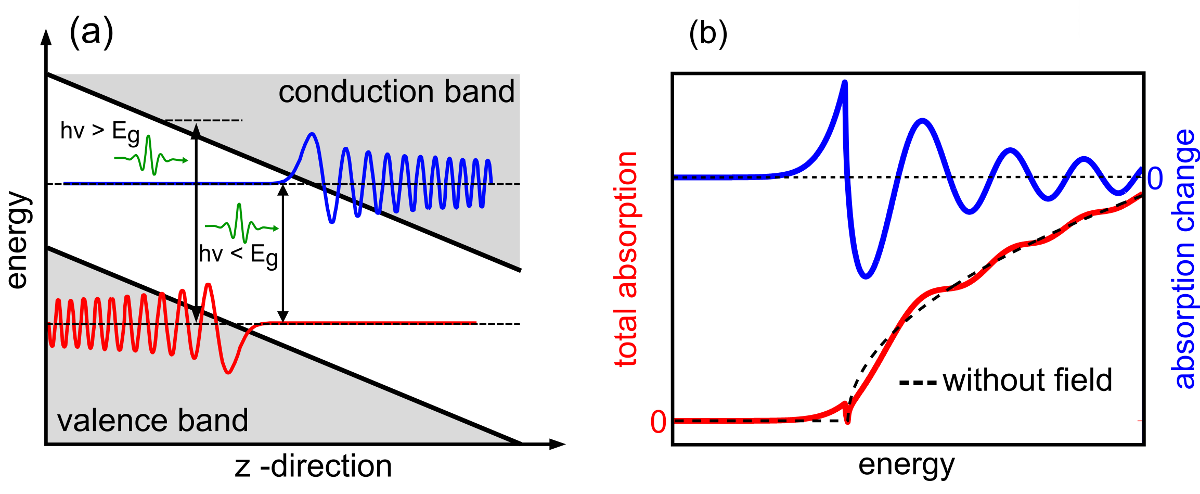
In aktuellen Experimenten werden die technologisch relevanten Hochgeschwindigkeits-Halbleiter Galliumarsenid (GaAs) und Indiumphospid (InP) untersucht. Dabei zeigt sich eine Fülle von sehr interessanten Phänomenen. Das intensive THz-Feld führt zu einer instantanen Abnahme der Transmission für Photonen mit Energien kleiner und zu einer induzierten Transmission für Photonenenergien größer als die Bandlückenenergie. Diese Signaturen sind starke Indizien für die erstmalige Beobachtung des dynamisch aufgelösten Franz-Keldysh-Effekts [16]. Des Weiteren zeigt sich eine effiziente Ladungsträgergeneration durch Tunnel- und Stoßionisation. Die dadurch generierte hohe Dichte an freien Elektronen führt zu weiteren, langlebigeren Effekten. Dazu gehören die Bandkantenrenormierung und die Pauli-Blockade.
Referenzen
[1] R. Huber, F. Tauser, A. Brodschelm, M. Bichler, G. Abstreiter und A. Leitenstorfer
"How many-particle interactions develop after ultrafast excitation of an electron–hole plasma"
Nature 414, 286 (2001)
[2] A. Pashkin, M. Porer, M. Beyer, K. W. Kim, A. Dubroka, C. Bernhard, X. Yao, Y. Dagan, R. Hackl, A. Erb, J. Demsar, R. Huber und A. Leitenstorfer
"Femtosecond Response of Quasiparticles and Phonons in Superconducting YBa2Cu3O7-δ Studied by Wideband Terahertz Spectroscopy"
Phys. Rev. Lett. 105, 067001 (2010)
[3] T. Kampfrath, A. Sell, G. Klatt, A. Pashkin, S. Mährlein, T. Dekorsy, M. Wolf, M. Fiebig, A. Leitenstorfer und R. Huber
"Coherent terahertz control of antiferromagnetic spin waves"
Nature Photon. 5, 31 (2010)
[4] C. Kübler, R. Huber und A. Leitenstorfer (eingeladener Artikel)
"Ultrabroadband terahertz pulses: generation and field-resolved detection"
Semicond. Sci. Technol. 20, 128 (2005)
[5] R. Huber, A. Brodschelm, F. Tauser und A. Leitenstorfer
"Generation and field-resolved detection of femtosecond electromagnetic pulses tunable up to 41 THz"
Appl. Phys. Lett. 76, 3191 (2000)
[6] A. Sell, A. Leitenstorfer und R. Huber
"Phase-locked generation and field-resolved detection of widely tunable terahertz pulses with amplitudes exceeding 100 MV/cm"
Opt. Lett. 33, 2767 (2008)
[7] A. Sell, R. Scheu, A. Leitenstorfer und R. Huber
"Field-resolved detection of phase-locked infrared transients from a compact Er:fiber system tunable between 55 and 107 THz"
Appl. Phys. Lett. 93, 251107 (2008)
[8] F. Junginger, A. Sell, O. Schubert, B. Mayer, D. Brida, M. Marangoni, G. Cerullo, A. Leitenstorfer und R. Huber
"Single-cycle multiterahertz transients with peak fields above 10 MV/cm"
Opt. Lett. 35, 2645 (2010)
[9] K. W. Kim, A. Pashkin, H. Schäfer, M. Beyer, M. Porer, T. Wolf, C. Bernhard, J. Demsar, R. Huber und A. Leitenstorfer
"Ultrafast transient generation of spin-density-wave order in the normal state of BaFe2As2 driven by coherent lattice vibrations"
Nature Materials 11, 497 (2012)
[10] F. Junginger, B. Mayer, C. Schmidt, O. Schubert, S. Mährlein, A. Pashkin, R. Huber und A. Leitenstorfer
wird publiziert
[11] A. Leitenstorfer, S. Hunsche, J. Shah, M. C. Nuss und W. H. Knox
"Femtosecond Charge Transport in Polar Semiconductors"
Phys. Rev. Lett. 82, 5140 (1999)
[12] Y. Yacoby
"High-Frequency Franz-Keldysh Effect"
Phys. Rev. 169, 610 (1968)
[13] G. H. Wannier
"Dynamics of Band Electrons in Electric and Magnetic Fields"
Rev. Mod. Phys. 34, 645 (1962)
[14] A. H. Chin, O. G. Calderon und J. Kono
"Extreme Midinfrared Nonlinear Optics in Semiconductors"
Phys. Rev. Lett. 86, 3292 (2001)
[15] K. Nordstrom et al.
"Excitonic Dynamical Franz-Keldysh Effect"
Phys. Rev. Lett. 81, 457 (1998)
[16] P. Y. Yu, und M. Cardona
"Fundamentals of Semiconductors"
Fourth Edition Springer, Berkely, CA and Stuttgart, Germany (March 2010)
