
Introduction
Laser and amplifier systems based on optical fibers have developed a versatile field of applications. The most established systems are based on fibers doped with the rare earth metal Erbium (Er). The large gain bandwidth of Er3+ ions, centered at a wavelength of 1550 nm, enables the generation of short pulses with a length of less than 100 fs (1 fs = 10-15 s). By precisely exploitating nonlinear effects it is possible to reach a pulse duration of just a few femtoseconds. Erbium:fiber amplifiers are widely used in telecommunication technology. As a consequence, many compact and low-cost standard components for such systems are available.
It is possible to generate tailored, tunable spectra in the wavelength region from 800 nm to 2400 nm for various applications via frequency conversion in highly nonlinear germanosilicate fibers (HNF). Depending on Germanium doping and waveguide design, these fibers have different dispersion properties. With the knowledge of these properties it is possible to calculate optimized fiber assemblies for the generation of tailored super continua [1]. In that way, it is possible to even synthesize short pulses with duration of just 4.3 fs via the coherent superposition of two independent spectra [2]. This time interval corresponds to exactly a single cycle for the electric field at the carrier wavelength of 1.3 µm.
In addition, the nonlinear effect of difference frequency generation opens an elegant way to passively stabilize the relative phase between the electric field and the pulse envelope, so that every pulse is an exact copy of the previous one [3].
Setup of a typical system
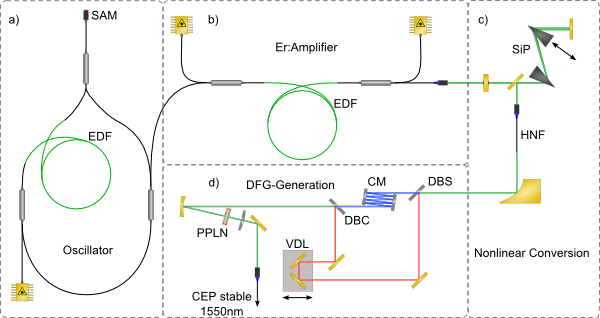
Figure 2 shows the setup of an Erbium-doped fiber laser system for frequency conversion (a) to (c) and generation of phase-locked pulses (d). It consists of a mode locked Er:fiber oscillator in a hybrid design of a linear and a circular part (Figure 2a). For mode locking, a saturable absorber mirror (SAM) is used in the linear part [4]. The oscillator is pumped by a laser diode at a wavelength of 974 nm , coupled in by a fiber-based beam splitter (WDM). The use of polarization-maintaining components results in an excellent stability.
The pulse energy of typically 60 pJ of the oscillator is not sufficient to efficiently drive significant processes in nonlinear optics. Via an amplifier, also based on an erbium-doped fiber, the pulse energy can be enhanced easily by more than three orders of magnitude. To this end, the amplifier is pumped from both sides with fiber-coupled laser diodes (Figure 2b).
A typical spectrum and the temporal characteristics of the output pulses of an amplifier are shown in Figure 3. In the silicon prism compressor (Figure 2c), the pulses are compressed to a duration of 120 fs. At the output pulse energy of around 10 nJ, field intensities are high enough for frequency conversion e.g. in a highly nonlinear fiber.
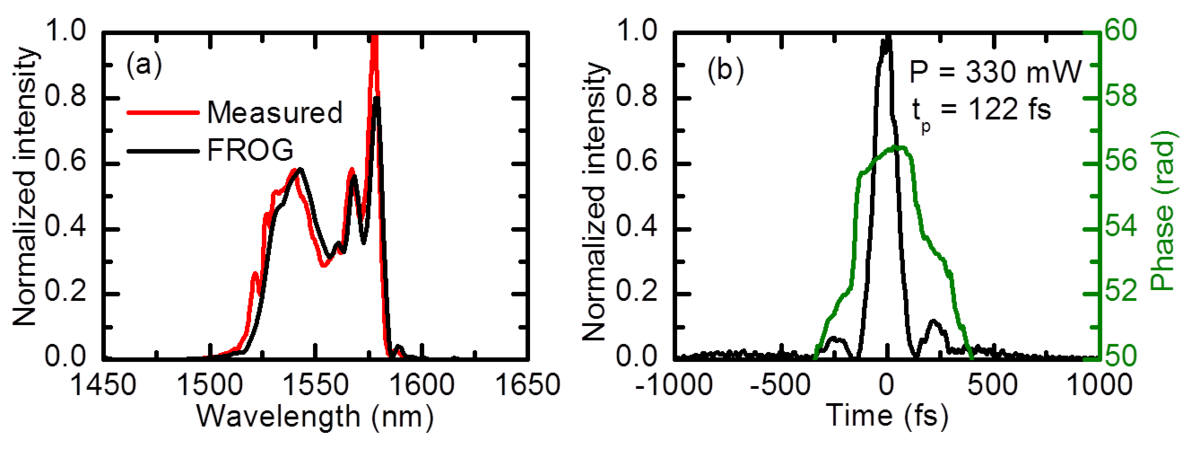
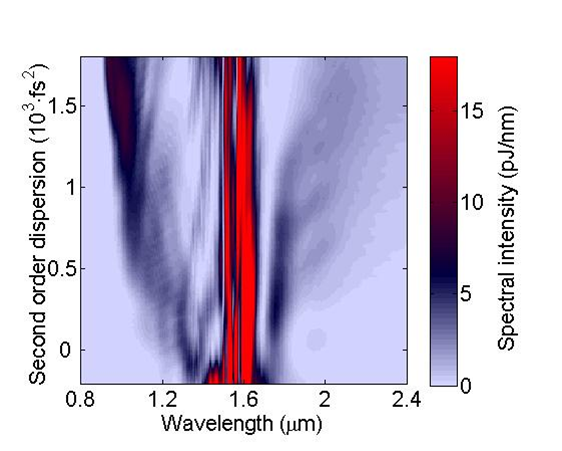
It is possible to reliably predict the pulse propagation in highly nonlinear fibers with a simulation program based on the nonlinear Schrödinger equation [5]. To this end, precise knowledge of the dispersion properties of the fibers is required in a broad wavelength range. These data are measured by a fiber-based white-light interferometer. Moreover, the input parameters of the pulses are known from FROG1 measurements. Parameter-free simulations are possible in this way (Figure 4). The calculated data are in excellent agreement with the experiments (Figure 5).
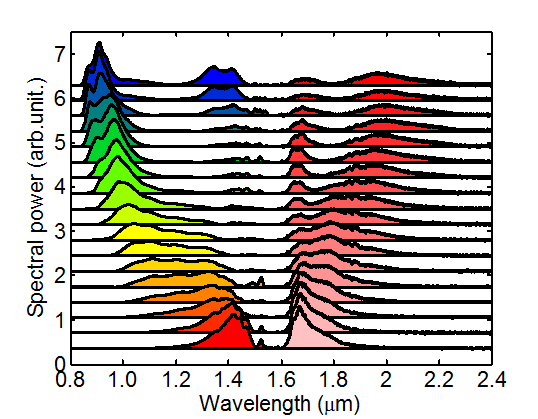
Typically, a combination of different fibers is used for efficient frequency conversion. The length of the first fiber is chosen in the way that short pulses with a duration of 20 fs are provided after solitonic compression, resulting in a peak power of 200 kW.
Typically, a combination of different fibers is used for efficient frequency conversion. The length of the first fiber is chosen in the way that short pulses with a duration of 20 fs are provided after solitonic compression, resulting in a peak power of 200 kW. Subsequently, the pulses break up in a piece of highly nonlinear fiber directly spliced to the precompression fiber, resulting in a short-wave part propagating dispersively, a long-wave solitonic pulse and the remaining pump light of a wavelength of 1550 nm [6]. The silicon prism compressor enables the tuning of the spectra over a wavelength region between 817 nm and 2200 nm via varying the pre-chirp of the input pulses.
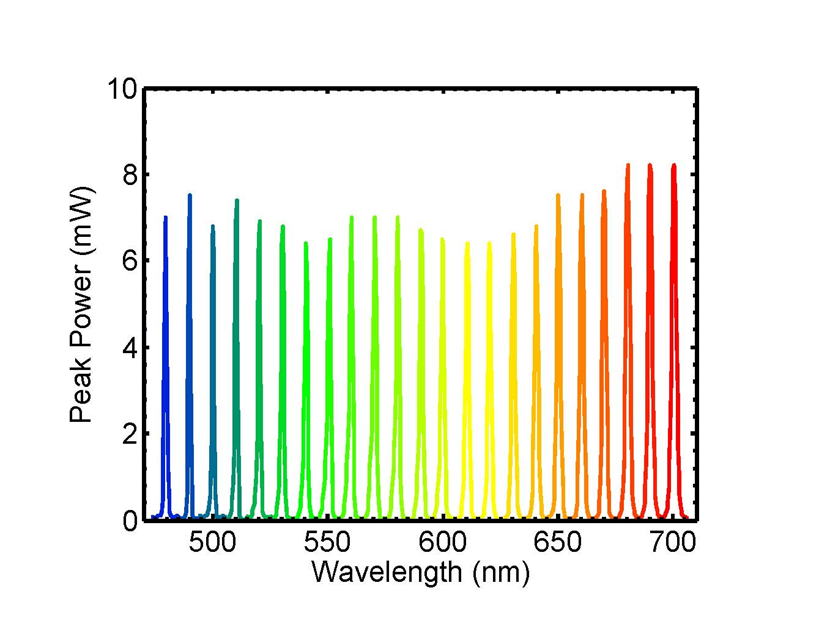
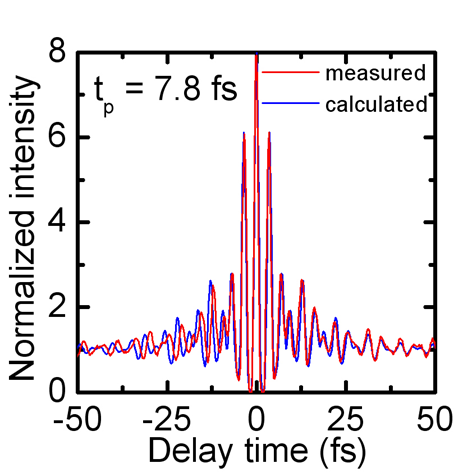
If the fiber combination is optimized for a broadband dispersive wave, pulse durations of 7.8 fs after compression can be reached [1]. The corresponding autocorrelation is shown in Figure 6. The entire visible spectral region from 450 nm to 700 nm becomes accessible via second-harmonic generation of the dispersive part in a fan-out lithium niobate crystal (Figure 7).
Generation of passively phase-locked pulses
The shorter the pulses, the more important becomes the phase relationship of the electric field relative to the envelope of a pulse - the so called carrier-envelope phase [7]. To generate identical pulses this parameter has to be kept constant. The passive stabilization of the carrier-envelope phase is implemented via difference frequency generation within a single frequency comb with a resulting wavelength of 1550 nm. This result is possible by using the dispersive and solitonic part of a spectrum out of the same highly nonlinear fiber (Figure 8). The use of just one HNF leads to an extremely stable system.
In Figure 2d) the setup for the generation of such phase-locked pulses is shown. Using a beam splitter the solitonic and dispersive parts can be split. For an efficient generation of the difference frequency, it is necessary to compress the short-wave part. This goal can be accomplished via chirped mirrors2. The tuning of the time delay of both spectral parts is achieved by a variable delay line.
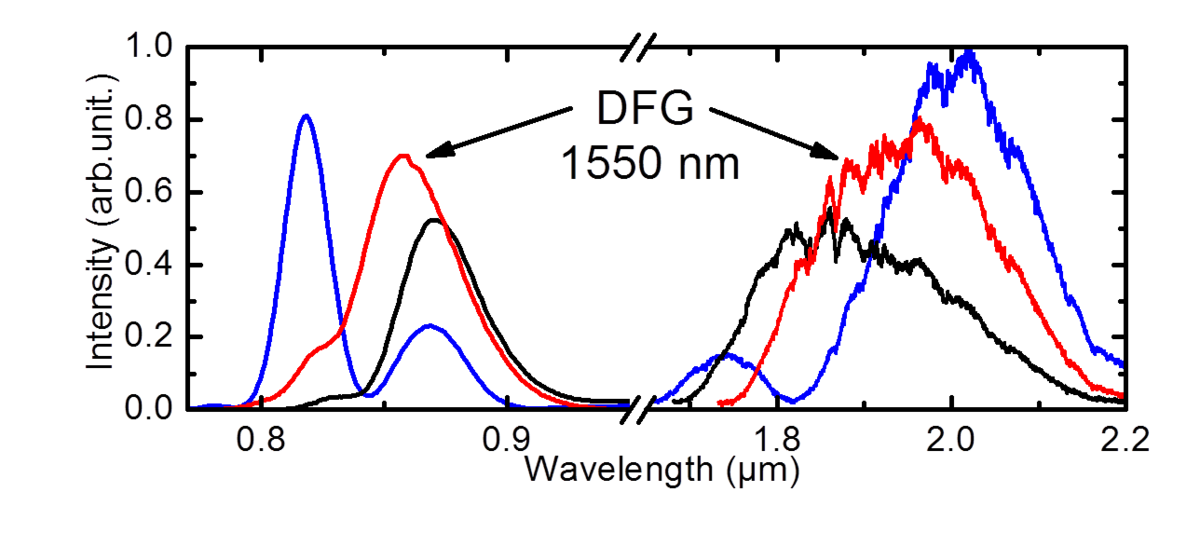
The difference frequency generation takes place in a periodically-poled lithium niobate crystal where the center wavelength is tunable between 1440 nm and 1700 nm. The pulses have a pulse energy of 50 pJ after the crystal. They are amplified to pulse energies around 10 nJ in another Er:fiber amplifier. Subsequent compression leads to pulses of a duration of 120 fs. These values are comparable to the pulse parameters after the first amplifier. Thus, this setup opens the possibility to drive nonlinear processes like temporal compression and frequency shifting in additional highly nonlinear fibers, but now with absoltue stability of the carrier-envelope phase [3].

With an f-2f-interferometer it can be demonstrated that changes in the phase position of each single light oscillation over a time of 8 s are smaller than 3.5 %. This value corresponds to an rms deviation of just 0.219 rad (figure 9 (c) and (d)). For this measurement, frequency components spanning more than one octave are generated in a HNF. The entire spectrum shares the same frequency comb. The short-wave part can be delayed by inserting dispersion via a slab of SF-66 glass. If one generates the second harmonic of the long-wave part, both spectra are at the same frequency. If the pulses are phase-locked to a carrier-envelop offset frequency of zero, a stable modulation may be seen in a spectrometer. Figure 9 (a) and (b) shows a measurement averaged over 160.000 pulses. The stationary spectral modulation proofs that the pulses have an excellent phase stability on a millisecond time scale.
To generate pulses in the physical limit of a single oscillation of the electric field, the compression of coherent radiation in an ultrabroad spectrum is necessary. The gain bandwidth of typical laser materials is not sufficient for this task and an extreme broadening for example due to self-phase modulation is required. The greatest challenge for this experiment is to support the coherence of all parts of the spectrum and to find a suitable method to compress the pulses at the same time.
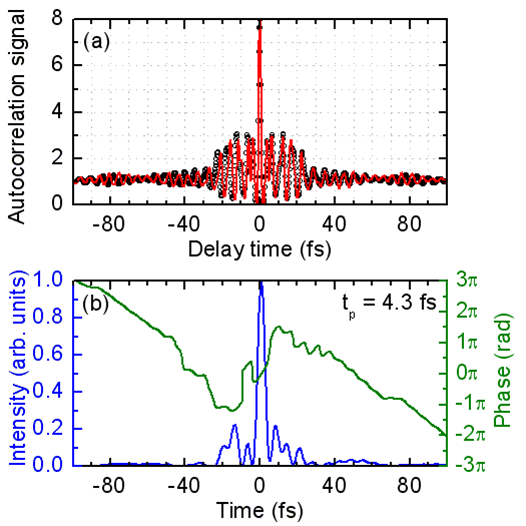
The highly flexible Er:fiber technology opens a new approach: two different amplifier branches are used, which are seeded by the same oscillator. Therefore, two different spectra can be generated in HNFs which are broadened and located in close spectral vicinity. From the first branch the solitonic part and from the second one the dispersive part is used. Both spectra are compressed in a separate glass prism compressor and coherently overlapped by a variable delay line. An autocorrelation and the result of a FROG measurement of the overlapped pulses are shown in Figure 10. The resulting pulse duration of 4.3 fs corresponds exactly to a single oscillation period of the electric field for the carrier wavelength of 1300 nm [2]. Therefore, it was possible for the first time to generate a single cycle of light. For example, these pulses are suitable for pump-probe spectroscopy with sub-femtosecond temporal resolution. In combination with the passive phase stabilization, the generation of attosecond pulses at the full repetition rate of the oscillator in the MHz regime appears feasible. Higher pulse energies are necessary in order to reach the required electric field amplitudes (see next section).
Applications for ultrabroad fiber lasers
For experiments in extremely nonlinear optics, pulse energies in the range of some µJ are necessary. Ytterbium (Yb) doped fiber amplifiers are typically used to reach such high pulse energies and average powers [8]. The technology of the passive phase locking can be extended to such applications. With the help of a HNF it is possible to shift the spectrum of the pulses to the wavelength region around 1030 nm, which corresponds to the gain maximum of Yb-doped fibers.
These stable and extreme flexible fiber lasers play an important role also in other areas. Examples are the generation of tailored spectra for nonlinear spectroscopy of optical nanoantennas [9] as well as ultrabroadband terahertz detection with highest sensitivity. The technology of passively phase-locked pulses is central also for the generation of frequency combs for space applications.
Current projects
- extension of the technology of the phase-stable pulses into new frequency regions and to higher pulse energies in the µJ regime
- implementation of a system with phase-locked pulses at a high repetition rate for generation of a frequency comb for space applications
- detection of multi-THz pulses with highest sensitivity at the quantum limit
References
[1] A. Sell, G. Krauss, R. Scheu, R. Huber und A. Leitenstorfer
"8-fs pulses from a compact Er:fiber system: quantitative modeling and experimental implementation"
Opt. Express 17, 1070 (2009)
[2] G. Krauss, S. Lohss, T. Hanke, A. Sell, S. Eggert, R. Huber und A. Leitenstorfer
"Synthesis of a single cycle of light with compact erbium-doped fibre technology"
Nature Photon. 4, 33 (2010)
[3] G. Krauss, D. Fehrenbacher, D. Brida, C. Riek, A. Sell, R. Huber und A. Leitenstorfer
"All-passive phase locking of a compact Er:fiber laser system"
Opt. Lett. 36, 540 (2011)
[4] F. Adler
"Erbium-dotierte Femtosekunden-Faserlaser und Anwendungen"
Doktorarbeit an der Universität Konstanz (2007)
[5] G. P. Agrawal
"Nonlinear Fiber Optics"
4th ed., Academic Press, San Diego (2007)
[6] F. Tauser, F. Adler und A. Leitenstorfer
"Widely tunable sub-30-fs pulses from a compact erbium-doped fiber source"
Opt. Lett. 29, 516 (2004)
[7] D. J. Jones, S. A. Diddams, J. K. Ranka, A. Stentz, R. S. Windeler, J. L. Hall und S. T. Cundiff
"Carrier-Envelope Phase Control of Femtosecond Mode-Locked Lasers and Direct Optical Frequency Synthesis"
Science 288, 635 (2000)
[8] Y. Jeong, J. Sahu, D. Payne und J. Nilsson
"Ytterbium-doped large-core fiber laser with 1.36 kW continuous-wave output power"
Opt. Express 12, 6088 (2004)
[9] T. Hanke, G. Krauss, D. Träutlein, B. Wild, R. Bratschitsch und A. Leitenstorfer
"Efficient Nonlinear Light Emission of Single Gold Optical Antennas Driven by Few-Cycle Near-Infrared Pulses"
Phys. Rev. Lett. 103, 257404 (2009)
[10] G. Krauss, T. Hanke, A. Sell, D. Träutlein, A. Leitenstorfer, R. Selm, M. Winterhalder und Andreas Zumbusch
"Compact coherent anti-Stokes Raman scattering microscope based on a picosecond two-color Er:fiber laser system"
Opt. Lett. 34, 2847 (2009)
[11] R. Selm, M. Winterhalder, A. Zumbusch, G. Krauss, T. Hanke, A. Sell und A. Leitenstorfer
"Ultrabroadband background-free coherent anti-Stokes Raman scattering microscopy based on a compact Er:fiber laser system"
Opt. Lett. 35, 3282 (2010)
